Implementasi Algoritma Heap Sort dengan C#

Untuk mengimplementasikan algoritma Heap sort pada postingan ane yg ini menggunakan bahasa pemrograman C#, gunakanlah syntax berikut ini :

using System;
using System.Text;

namespace research
{
 class Heap
 {
  public void HeapSort()
  {
   Console.Clear();
   Console.WriteLine("Masukkan banyak elemen yang anda inginkan : ");

   /* Proses validasi input user */
   string Input = Console.ReadLine();
   int Elements;
   if(int.TryParse(Input, out Elements))
   {
    Elements = Convert.ToInt32(Input);
   }
   else
   {
    Console.WriteLine("Maaf anda melakukan input yang salah, silahkan tekan enter untuk mengulangi");
    Console.ReadLine();
    HeapSort();
   }
   

   /* Deklarasi Array Angka */
   int[] Angka = new int[Elements];
   int Result = Elements;
   Console.WriteLine("------------------------------------------------");

   /* Input nilai pada elemen-elemen di Array */
   for(int i=0; i < Elements; i++)
   {
    Console.WriteLine("Silahkan masukkan angka untuk mengisi elemen " + i + ":");
    string Input_Temp = Console.ReadLine();
    int nilai;
    if(int.TryParse(Input_Temp, out nilai))
    {
     Angka[i] = Convert.ToInt32(nilai); 
    }
    else
    {
     Console.WriteLine("Maaf anda melakukan input yang salah, silahkan tekan enter untuk mengulangi");
     Console.ReadLine();
     HeapSort();
    }
    
   }

   /* Menggunakan metode Build_Max_Heap() */
   Build_Max_Heap(Angka, Elements);

   /* Metode untuk Heap Sort */
   for(int i=Elements - 1; i > 0; i--)
   {
    int Temp = Angka[i];
    Angka[i] = Angka[0];
    Angka[0] = Temp;

    Elements--;
    Max_Heapfy(Angka, Elements, 0);
   }

   /* Metode untuk menampilkan hasil sorting */
   Console.WriteLine("---------------------------");
   Console.WriteLine("Hasil sorting adalah : ");

   for(int i=0; i < Result; i++)
   {
    Console.WriteLine("{0,1} {1,2}", "Elemen " + i + ":", Angka[i]);
   }
  }

  public void Build_Max_Heap(int[] Angka, int Elements)
  {
   for(int i=(Elements - 1) / 2; i >= 0; i--)
   {
    /* Menggunakan metode Max_Heapfy() */
    Max_Heapfy(Angka, Elements, i);
   }
  }

  public void Max_Heapfy(int[] Angka, int Elements, int Index)
  {
   int left = (Index + 1) * 2 - 1;
   int right = (Index + 1) * 2;
   int largest;

   if(left < Elements && Angka[left] > Angka[Index])
   {
    largest = left;
   }
   else
   {
    largest = Index;
   }

   if(right < Elements && Angka[right] > Angka[largest])
   {
    largest = right;
   }

   if(largest != Index)
   {
    int Temp = Angka[Index];
    Angka[Index] = Angka[largest];
    Angka[largest] = Temp;

    Max_Heapfy(Angka, Elements, largest);
   }
  }


  static void Main(string[] args)
  {
   Heap H = new Heap();
   H.HeapSort();
  }
 }
}

Pada syntax ini terdapat 3 metode yang digunakan dalam sorting nilai dengan algortima heap sort yaitu HeapSort, Build-Max-Heap, dan Max-Heapfy. Pada metode HeapSort di baris 10 sampai 50 adalah metode untuk deklarasi array Angka dan input nilai pada elemen-elemen yang dimiliki array Angka. Lalu pada baris 51 metode Build-Max-Heap dipanggil untuk mengkoreksi posisi heap tree agar sesuai dengan kondisi Max-Heap, pada metode Build-Max-Heap di baris 78 terdapat for looping dengan kondisi i = (Elements – 1) / 2 dan selama i ≥ 0 for looping akan terus berulang berarti posisi i berada di tengah-tengah heap tree. Pada posisi i adalah index awal yang akan dijadikan acuan untuk mengkorekasi posisi heap tree agar sesuai dengan max-heap setelah index tengah sudah ditemukan maka cara untuk mengkoreksi posisi heap adalah dengan metode Max-Heapfy.

Pada metode Max-Heapfy terapat variabel left, right, dan largest. Dimana left dan right adalah variabel index left dan right child dari node i sedangkan variabel largest digunakan untuk menentukan index mana yang memiliki nilai tertinggi antara node i, left child, dan right child node i. Maka pada metode Max-Heapfy index yang tersimpan dalam variabel largest akan menjadi parent node atau node i, akan tetapi jika largest ≠ i maka metode Max-Heapfy akan kembali memanggil dirinya sendiri karena jika largest ≠ I urutan heap tree tidak sesuai dengan kondisi max-heap.

Lalu setelah Max-Heap sudah terbentuk kembali ke metode HeapSort dimana terdapat for lopping yang memiliki kondisi i = Elements – 1 dan selama i > 0 maka i dikurangi 1. Dan didalam for looping nilai pada index 0 atau root ditukar dengan nilai pada index n atau index terakhir setelah itu jumlah elemen akan dikurangi 1 dan metode heapsort memanggil metode metode Max-Heapfy untuk mengkoreksi urutan heap tree agar sesuai dengan kondisi Max-Heap. Dan berikut adalah demo dari pengaplikasian metode HeapSort dengan C# :

Sekian postingan dari ane semoga bermanfaat, jika ada kesalahan mohon dikoreksi dan dimaklumai :Peace:

Algoritma Heap Sort

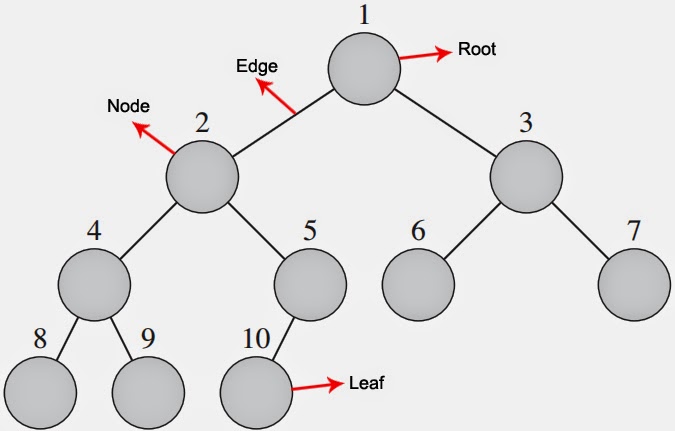
Heap sort adalah sebuah metode sorting (pengurutan) angka pada sebuah array dengan cara menyerupai binary tree, yaitu dengan cara memvisualisasikan sebuah array menjadi sebuah binary tree yang nantinya pada binary tree tersebut nilai pada masing-masing index array akan diurutkan. Pada heap sort terdapat 3 bagian yaitu Node, Edge, dan leaf dimana node itu adalah setiap index yang berada pada array, edge adalah garis yang menghubungkan tiap node dan leaf adalah setiap node yang tidak memiliki child node (node turunan). Selain itu juga ada yang bernama root yaitu node awal pada sebuah heap, berikut adalah ilustrasi dari bagian yang dimiliki oleh heap :

Heap tree terbagi menjadi 2 jenis yaitu Max-Heap dan Min-Heap, dimana max-heap adalah kondisi heap tree yang memiliki nilai tertinggi berada di node root dan setiap child node memiliki nilai yang lebih kecil dari nilai yang dimiliki parent nodenya. Sedangkan pada min-heap adalah kondisi kebalikan dengan max-heap, pada min-heap nilai terkecil berada di node root dan setiap child node memiliki nilai yang lebih besar dari nilai yang dimiliki parent nodenya. Pada metode heap sort jenis heap tree yang digunakan adalah Max-Heap.

Dan untuk memvisualisasikan sebuah array menjadi sebuah heap tree adalah dengan cara mencari node root terlebih dahulu yaitu node pertama node pertama sebuah heap tree adalah index pertama di array yaitu index 0 akan tetapi pada heap tree node awal berada di posisi 1 berbeda dengan array yang memiliki index awal yaitu index 0. Setelah node root telah ditemukan maka sekarang tinggal mencari child node dari node root dan child node terbagi menjadi 2 yaitu left child dan right child dan untuk mencari left child, right child, dan parent digunakan rumus sebagai berikut :

·         Left Child                        : 2i (Contoh : Left child dari 1 adalah 2 x 1 = 2)

·         Right Child                     : 2i + 1 (Contoh : Right Child dari 1 adalah (2 x 1) + 1 = 3)

·         Parent                              : └ i/2 ┘ (Contoh : Parent dari 3 adalah 3 / 2 = 1 )

NB : Untuk i adalah posisi node yang ingin dicari left/right childnya atau parent nodenya dan untuk lambing (└ ┘) adalah floor yaitu pembulatan kebawah missal 3 / 2 = 1,5 dibulatkan kebawah menjadi 1. Berikut adalah contoh cara memvisualisasikan sebuh array menjadi sebuah heap tree :

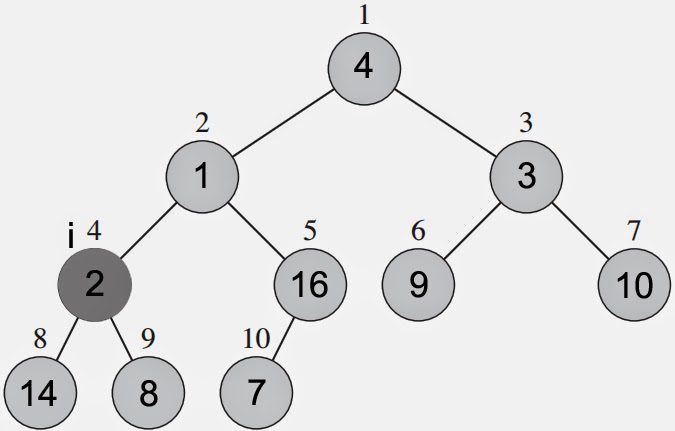
Contoh : Kita memiliki sebuah aray A = 4, 1, 3, 2, 16, 9, 10, 14, 8, 7. Dan untuk memvisualisasikan array tersebut gunakan rumus yang sudah disediakan dan prosesnya akan terlihat seperti ini :

Dan hasil heap treenya adalah sebagai berikut :   

Akan tetapi pada max-heap kondisi heap tree adalah node dengan nilai tertinggi adalah root dan setiap parent node memiliki nilai yang lebih besar dari child nodenya, dan heap tree yang terbentuk dari array A tidak memenuhi kondisi max-heap oleh karena itu dibutuhkan metode untuk membuat heap tree tersebut memiliki kondisi max-heap. Dalam metode sorting heap sort terdapat 2 metode yang digunakan yaitu Build-Max-Heap dan Max-Heapfy, Build-Max-Heap adalah metode yang digunakan untuk membuat heap tree diatas memenuhi kondisi dari max-heap, berikut ini adalah ilustrasi penggunaan metode HeapSort, Build-Max-Heap, dan Max-Heapfy pada sebuah heap tree :

HeapSort(A)

1.    Deklarasi array A

2.    Deklarasi Elemen

3.    Input elemen array A

4.    Input nilai-nilai elemen array A

5.    Build-Max-Heap(A)

6.    For i = Elemen – 1 selama i > 0

7.          Tukar A[i] dengan A[0]

8.          Elemen – 1

9.          Max-Heapfy(A, 1)

10. End for

Dapat dilihat pada algoritma HeapSort terdapat 2 metode yang dipanggil yaitu Build-Max-heap dan Max-Heapfy, dan algoritma dari Build-Max-heap adalah :

Build-Max-Heap(A)

1.    For i = (Elemen - 1) / 2 selama i ≥ 0

2.          Max-Heapfy(A, i)

3.    End for

Pada metode Build-Max-Heap terdapat for looping yang membagi 2 jumlah elemen, disini elemen – 1 karena pada array index awal adalah 0 sedangkan pada heap tree adalah 1, lalu elemen dibagi 2 dan selama i ≥ 0 maka for looping akan terus berajalan. Dan berikut adalah metode Max-Heapfy :

Max-Heapfy(A, i)

1.    Deklarasi left = (i + 1) * 2 – 1

2.    Deklarasi right = (i + 1) * 2

3.    Deklarasi largest

4.    if(left < elemen dan A[left] > A[i])

5.          largest = left

6.    end if

7.    else

8.          largest = i

9.    end else

10. if(right < elemen dan A[right] > A[i])

11.       largest = right

12. end if

13. if(largest != i)

14.       Tukar A[i] dengan A[largest]

15.       Max-Heapfy(A, i)

16. end if

 

Sebenarnya metode Max-Heapfy digunakan untuk mengkoreksi posisi dari index yang dipilih apakah posisinya sudah memenuhi kondisi Max-Heap yaitu tiap node parent harus memiliki nilai yang lebih tinggi dari nilai yang dimiliki child nodenya, dan dengan metode Max-Heapfy pengaturan posisi node yang memenuhi kondisi Max-Heap dapat dilakukan. Maka pada metode Build-Max-Heap banyaknya elemen array dibagi menjadi 2 dan hasil bagianya itu adalah lokasi index awal yang akan diperiksa apakah sudah memenuhi kondisi Max-Heap atau belum dan proses pemeriksaan dilakukan oleh metode Max-Heapfy. Berikut adalah ilustrasi penggunakan metode Build-Max-Heap :

Heap tree awal adalah seperti ini :

Karena pada heap tree jumlah node/elemen ada 10 (kalo di array adalah 9) maka jumlah elemen di bagi 2 (10 / 2 = 5 atau └ 9 / 2 ┘ = 4) maka yang menjadi variabel i adalah 5 (untuk heap tree) atau 4 (untuk array) maka ilustrasinya adalah sebagai berikut :

Karena node sebagai parent node sudah memiliki nilai lebih besar dari child nodenya (node 10) maka pertukaran posisi tidak terjadi, selanjutnya adalah lanjut ke index 4 :

Disini ternyata nilai yang dimiliki node 4 lebih kecil dari nilai yang dimiliki child nodenya (node 8 dan 9)  maka pertukaran posisi dilakukan dan hasilnya adalah sebagai berikut :

Selanjutnya adalah node 3 :

Disni node 3 memiliki nilai yang lebih kecil dari child nodenya (node 6 dan 7) maka pertukaran posisi dilakukan antara node 3 dan 7 karena antara node 3, 6, dan 7 node 7 lah yang memiliki nilai yang paling tinggi. Maka hasilnya adalah sebagai berikut :

 

Selanjutnya adalah node 2 :

Node 2 memiliki nilai yang lebih kecil dari child nodenya (node 4 dan 5) maka pertukaran posisi dilakukan disini node 5 memiliki nilai yang paling tinggi maka nilai pada index 2 bertukar posisi dengan nilai pada index 5. Maka hasilnya adalah sebagai berikut :

Setelah itu posisi index berubah menjadi pada node 5 dan ternyata disini nilai pada node 5 lebih kecil dari nilai yang berada di child nodenya yaitu node 10 maka perpindahan posisi kembali dilakukan dan hasilnya terlihat seperti ini :

Selanjutnya posisi index berada di node 1 :

Disini nilai pada index 1 lebih kecil dbandingkan dengan nilai yang dimiliki child nodenya (node 2 dan 3) maka nilai pada node 1 ditukar dengan nilai pada node 2 karena nilai pada node 2 adalah nilai tertinggi dari nilai pada 1 dan 3 dan hasilnya adalah :

Setelah pertukaran posisi sekarang posisi i ada di index 2 disini nilai pada index 2 lebih kecil dibandingkan nila yang dimiliki child nodenya (index 4 dan 5) maka pertukaran posisi kembali terjadi disini index 4 memiliki nilai tertinggi maka nilai pada indx i ditukar dengan nilai pada index 4 dan hasilnya adalah sebagai berikut :

Setelah proses tukar posisi selesai maka posisi i adalah di node 4 akan tetapi disini kembali nilai pada index i lebih kecil dibandingkan dengan nilai yang dimiliki child nodenya (node 9), maka nilai pada index i ditukar dengan nilai pada index 9 dan hasilnya adalah sebagai berikut  :

Sampai disini maka proes Build-Max-Heap telah selesai karena masing-masing parent node memiliki nilai yang lebih besar dari child nodenya, yaitu seperti heap tree berikut :

Setelah proses Build-Max-Heap telah selesai baru lah kita dapat menggunakan metode HeapSort untuk mengurutkan nilai pada array A. Pada algoritma heapsort setelah melakukan algoritma Build-Max-Heap nilai pada index terakhir i akan ditukar dengan node 1 atau root selama i > 0 disini nilai 16 akan ditukar dengan 1 dan jumlah elemen akan dikurangi 1 akan tetapi setelah perkukaran posisi dilakukan tree heap tidak memenuhi kondisi Max-Heap maka algoritma Max-Heapfy digunakan dan ilustrasinya adalah sebagai berikut :

Sampai pada tahap ini nilai tertinggi sudah berada di index yang benar index terakhir 10 pada heap tree dan 9 di array, langkah selanjutnya adalah mengulang cara yang sama dengan for looping selama  i > 0. Berikut adalah ilustrasi lengkapnya :

 

Maka setelah algoritma HeapSort dilakukan nilai-nilai pada array akan terurut dari nilai terkecil sampai terbesar. A = 1, 2, 3, 4, 7, 8, 9, 10, 14, 16. Dan berikut adalah flowchart untuk algoritma Heapsort :

Dan untuk implementasi algoritma heap sort, bisa dilihat dipostingan ane berikut ini :

Implementasi agoritma heap sort dengan C#

Sekian postingan ane semoga bermanfaat, klo ada yang salah mohon dikoreksi dan dimaklumi ya gan :Peace: